According to linear theory and assuming the liquids to be inviscid and the bubbles to remain spherical, bubbles set in oscillation attract or repel each other with a force that is proportional to the product of their amplitude of volume pulsations and inversely proportional to the square of their distance apart.
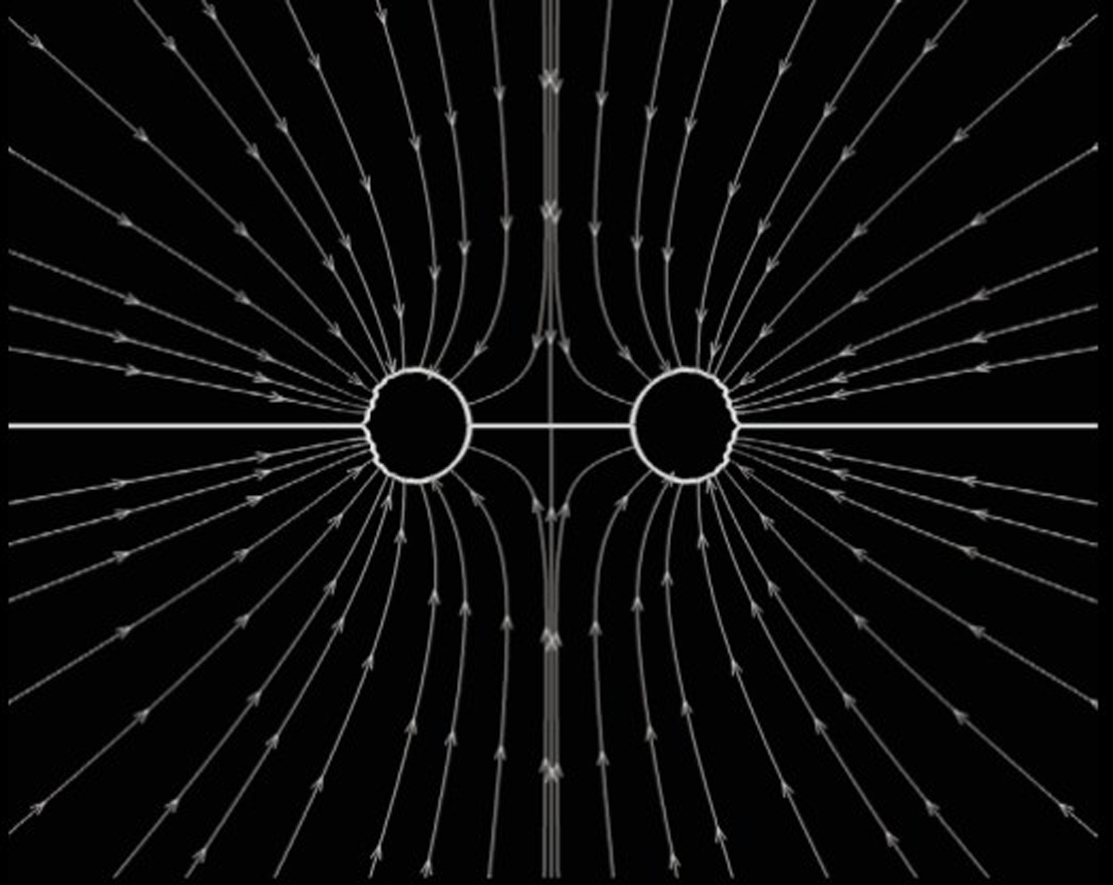
This force is attractive, if the forcing frequency lies outside the range of eigenfrequencies for volume oscillation of the two bubbles. Here we study the nonlinear interaction of two deformable bubbles set in oscillation in water by a step change in the ambient pressure, by solving the Navier–Stokes equations numerically.
As in typical experiments, the bubble radii are in the range 1–1000 μm. We find that the smaller bubbles (῀5 μm) deform only slightly, especially when they are close to each other initially. Increasing the bubble size decreases the capillary force and increases bubble acceleration towards each other, leading to oblate or spherical cap or even globally deformed shapes.

These deformations may develop primarily in the rear side of the bubbles because of a combination of their translation and harmonic or subharmonic resonance between the breathing mode and the surface harmonics. Bubble deformation is also promoted when they are further apart or when the disturbance amplitude decreases.
The attractive force depends on the Ohnesorge number and the ambient pressure to capillary forces ratio, linearly on the radius of each bubble and inversely on the square of their separation. Additional damping either because of liquid compressibility or heat transfer in the bubble is also examined.



